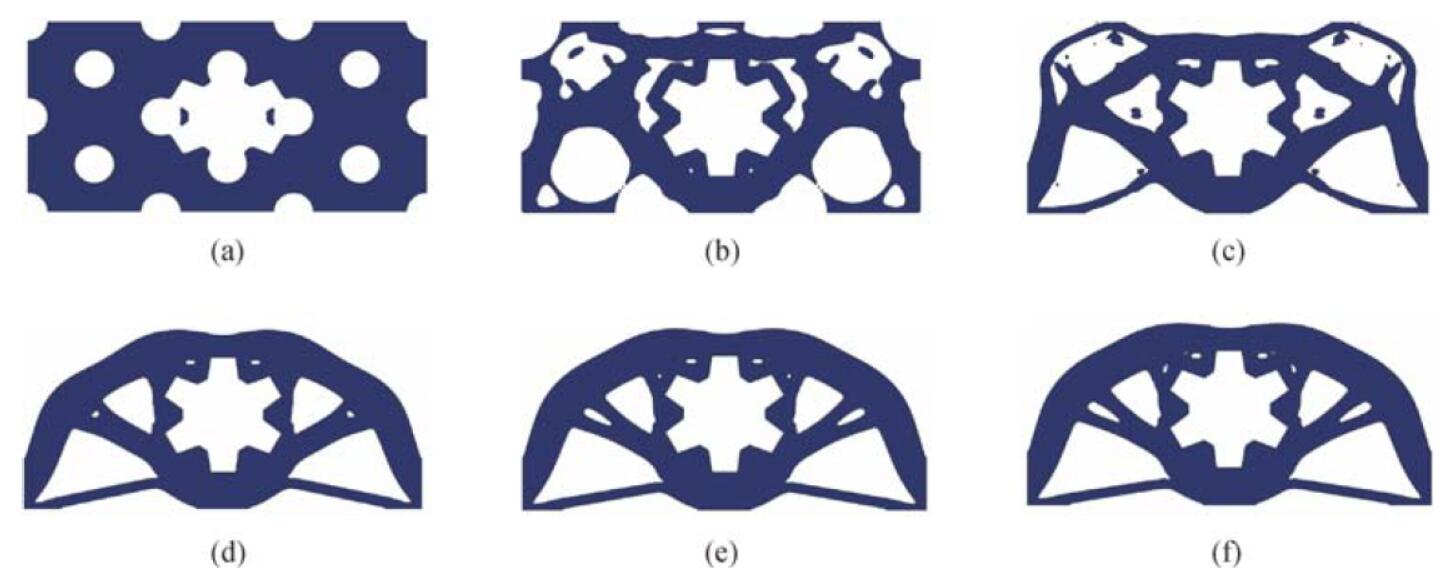
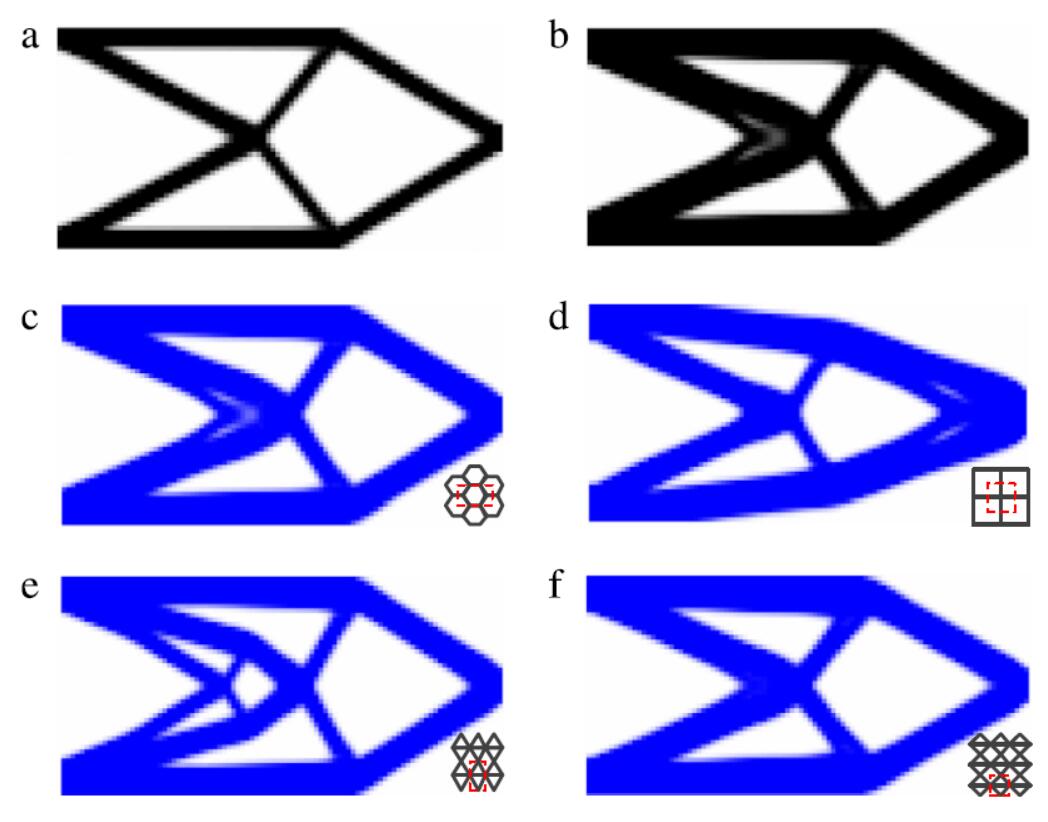
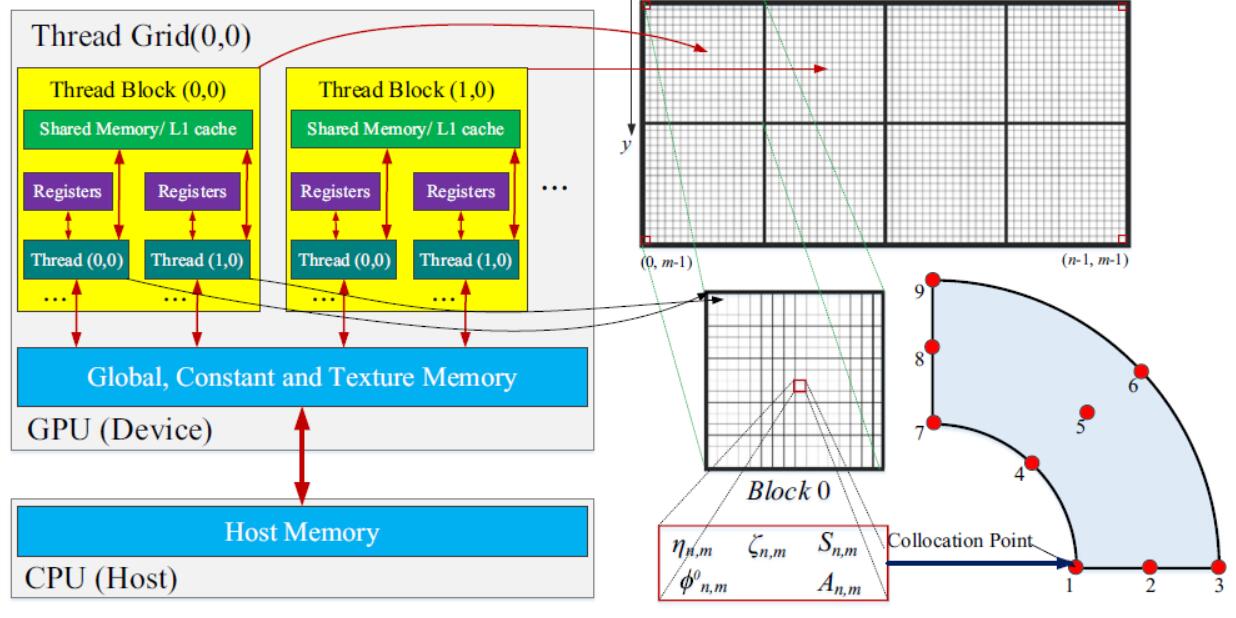
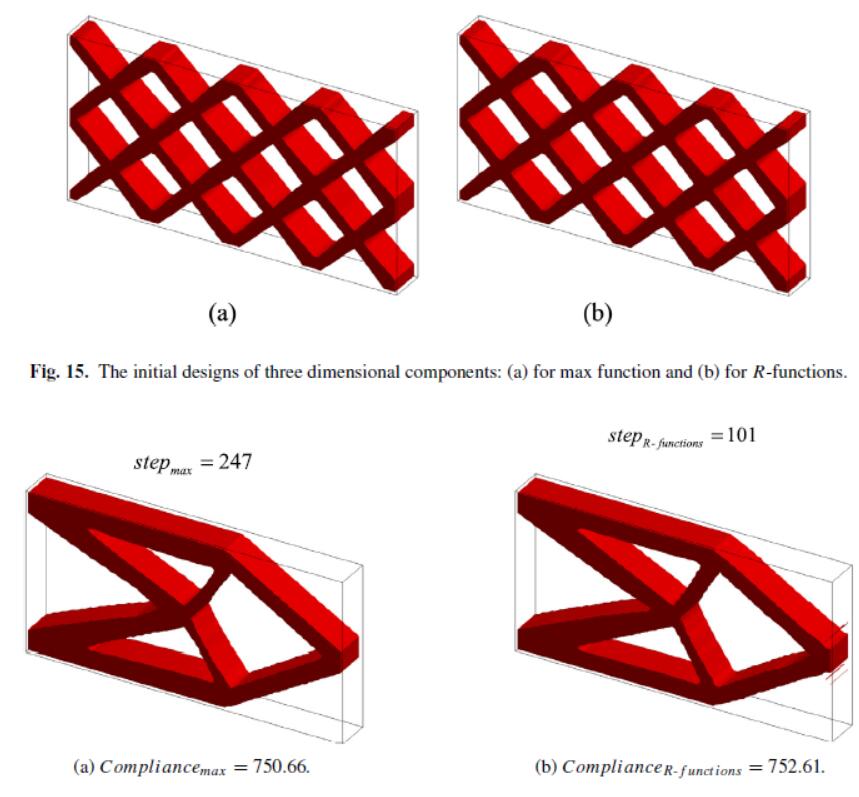
Geometrically constrained isogeometric parameterized level-set based topology optimization via trimmed elements
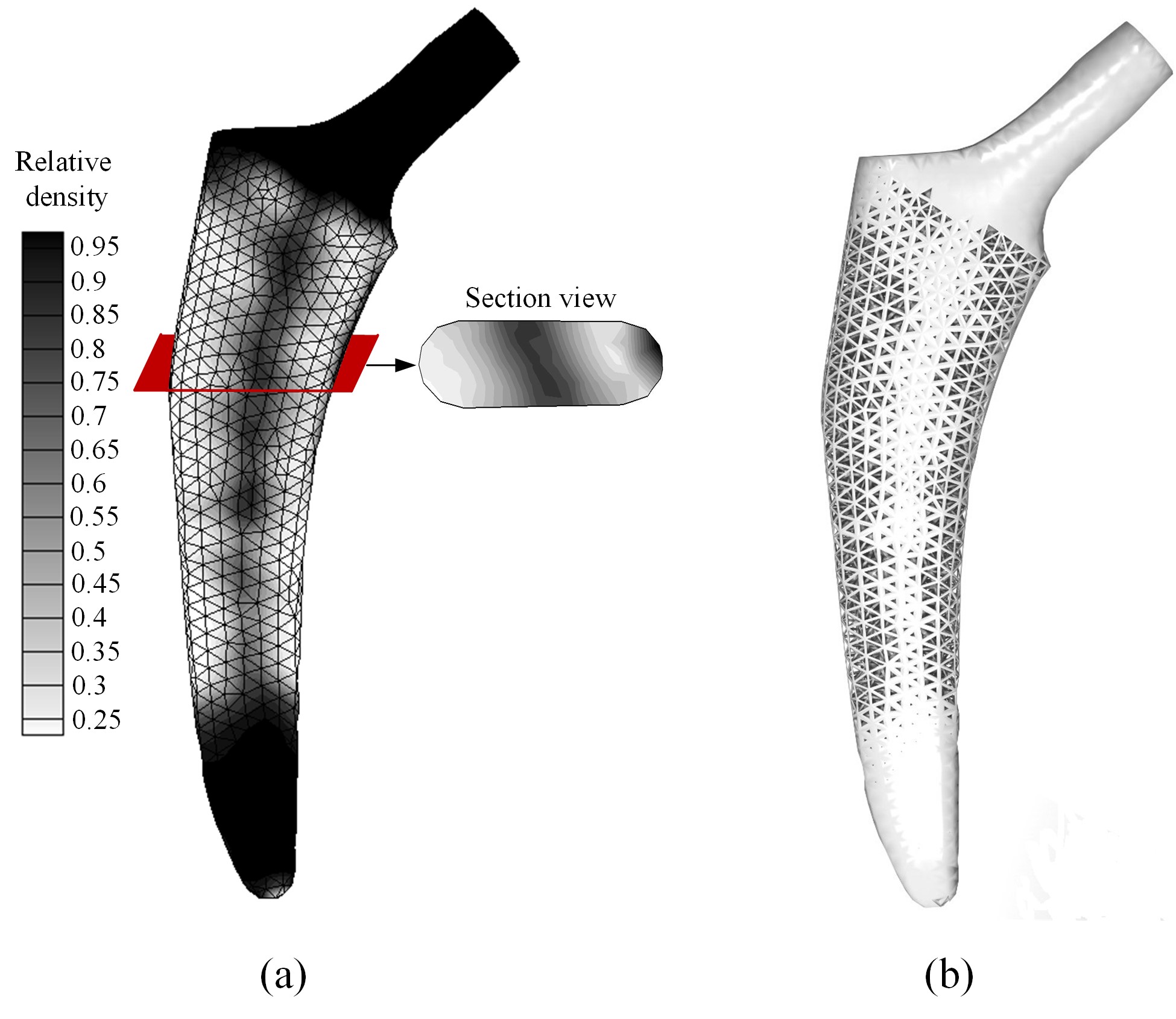
In this paper, an approach based on the fast point-in-polygon (PIP) algorithm and trimmed elements is proposed for isogeometric topology optimization (TO) with arbitrary geometric constraints. The isogeometric parameterized level-set-based TO method, which directly uses the non-uniform rational basis splines (NURBS) for both level set function (LSF) parameterization and objective function calculation, provides higher accuracy and efficiency than previous methods. The integration of trimmed elements is completed by the efficient quadrature rule that can design the quadrature points and weights for arbitrary geometric shape. Numerical examples demonstrate the efficiency and flexibility of the method.