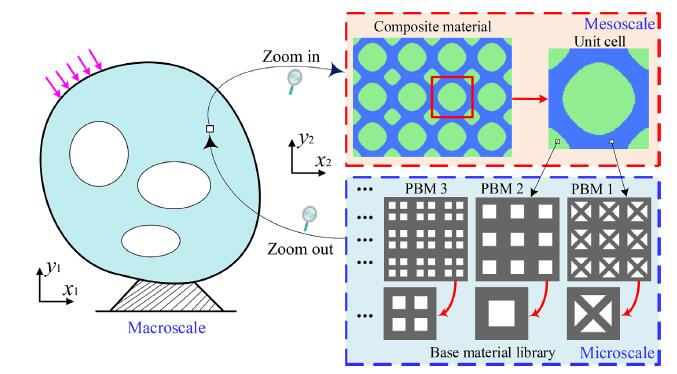
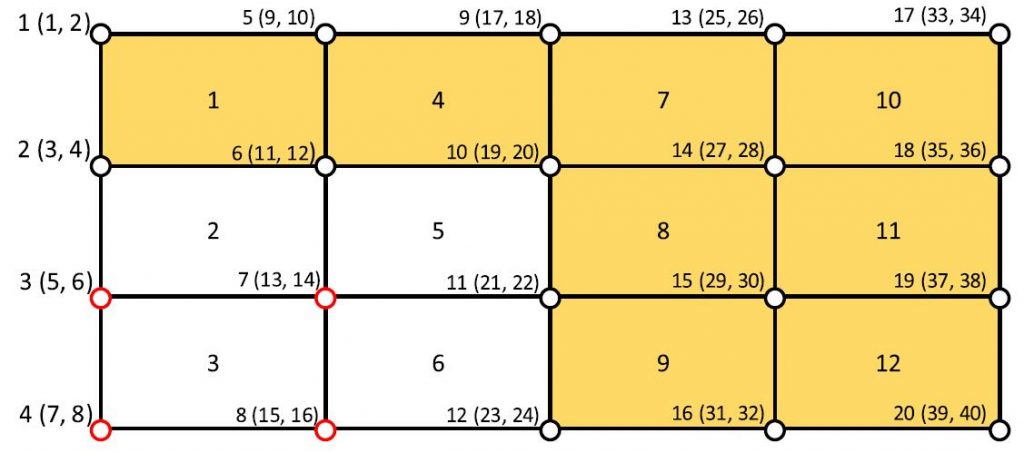
Hierarchical design of material microstructures with thermal insulation properties
Composite materials with multiple properties are important for a range of engineering applications. Hence, this study focuses on topological design of hierarchical materials with multiple performance in both thermal insulation and mechanics. First, a novel multi-objective optimization function is defined to find a solution from the Pareto frontier, where the weight coefficients can be adjusted adaptively, to keep all the individual objective functions and their sensitivities stabilized at the same level during the optimization. Second, a new design strategy is proposed to achieve the hierarchical designs of biphasic material microstructures, they are periodically arranged by the porous base materials that are known in advance and independent of topology optimization. Third, sensitivity information and algorithm im- plementation are given in detail, and the bi-directional evolutionary structural optimization method is adopted to iteratively update the micro-structural topologies, by combining with the homogenization method. Last, numerical examples are provided to illustrate the benefits of the proposed design method, such as high efficiency, implementation easiness, good connectivity and clear interface between adjacent phases, etc.