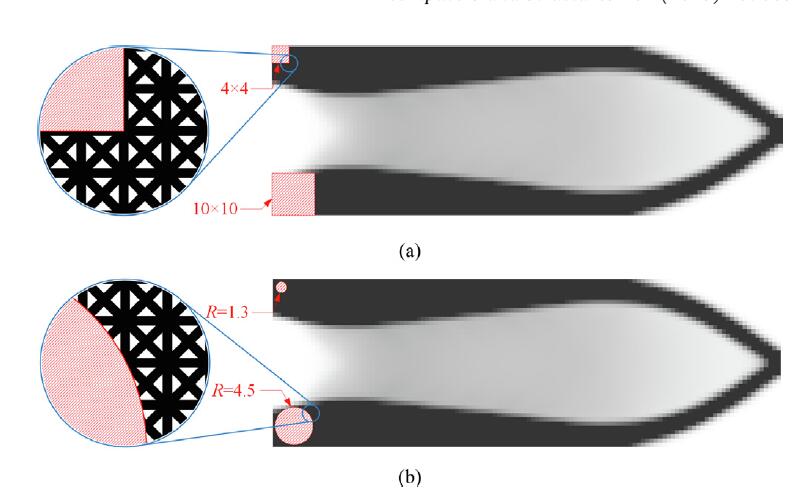
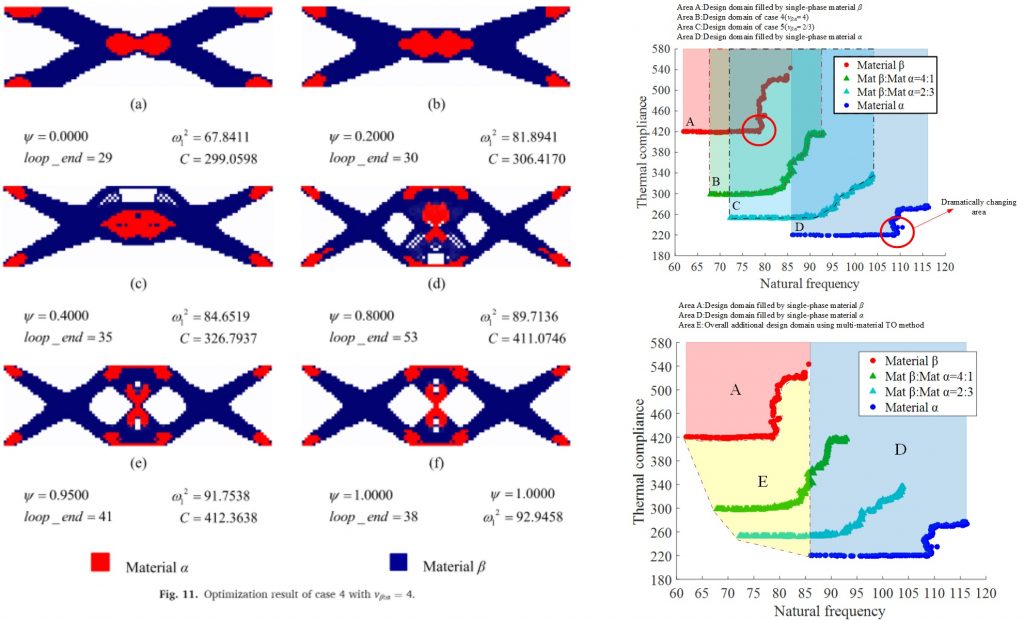
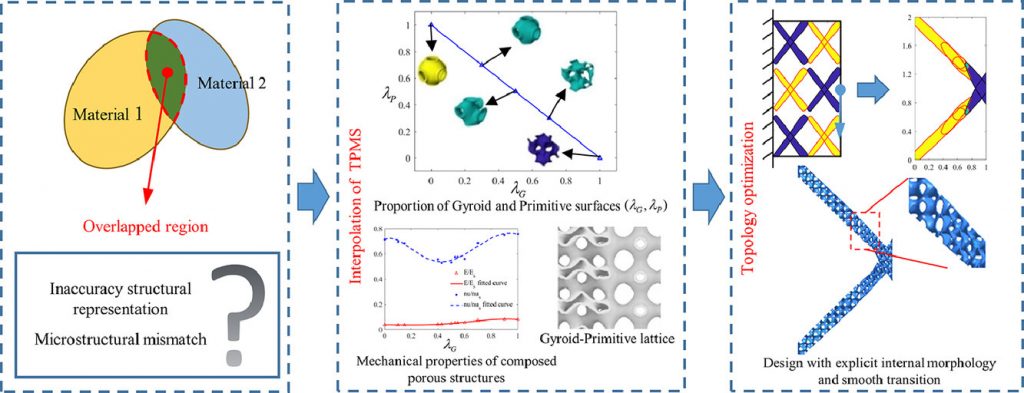
Fail-safe topology optimization for multiscale structures
This paper presents a novel fail-safe topology optimization method for multiscale structures. The partial
damage of both macroscopic and microscopic scales is considered for structural design. To ensure precision,
the effective elasticity tensor obtained by the homogenization method is fitted as a high-order polynomial
function. Meanwhile, the simplified models of partially damaged truss-like microstructure are
employed to reduce the computational cost and the difficulty of fitting. Moreover, Heaviside projection
is applied to speed up the convergence and yield a relatively clear configuration. Three numerical examples
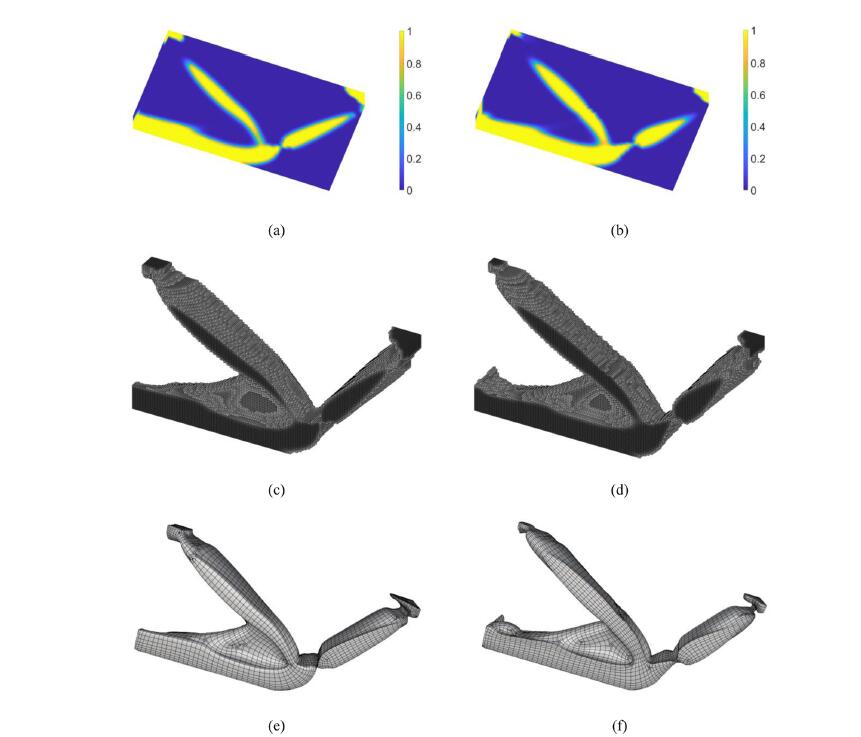
are tested to demonstrate that the optimized multiscale structures successfully obtain comprehensive
performances than optimized solid structures when appropriate microstructure configurations are
chosen. Besides, multiscale structures are more self-supporting than solid structures and thus more suitable
for additive manufacturing due to the large number of gray elements diffused