分类： 2020

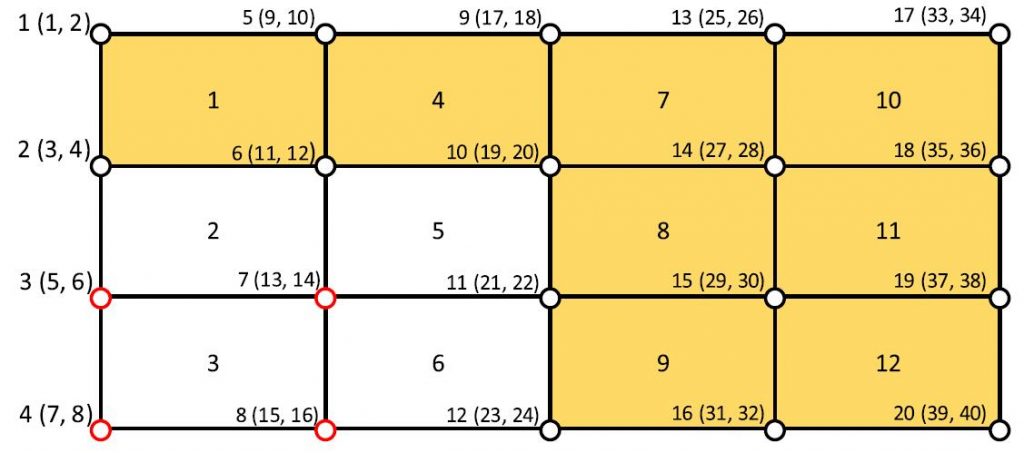
This paper proposes a highly efficient topology optimization using two accelerated methods, which can reduce the degrees of freedom (DOFs) of the finite element equations and accelerate the iteration convergence of the topology optimization. For the DOF reduction, a method based on the empty elements and the displacement change during the topology iterations is presented to remove the DOFs from the finite element equations. For the convergence acceleration, a gray-scale suppression method is proposed to accelerate the polarization of design variables which accelerates the iteration convergence of the topology optimization. Three numerical examples including 2D and 3D cases are tested, and the results show that the proposed method can significantly improve the efficiency of the topology optimization and obtain the optimization results with the same accuracy. The computational time is only about 7% – 29% compared to the conventional topology optimization method.

Focusing on the structural optimization of auxetic materials using data-driven methods, a back-propagation neural network (BPNN) based design framework is developed for petal-shaped auxetics using isogeometric analysis. Adopting a NURBS-based parametric modelling scheme with a small number of design variables, the highly nonlinear relation between the input geometry variables and the effective material properties is obtained using BPNN-based fitting method, and demonstrated in this work to give high accuracy and efficiency. Such BPNN-based fitting functions also enable an easy analytical sensitivity analysis, in contrast to the generally complex procedures of typical shape and size sensitivity approaches.

This paper proposes a new high-efficiency isogeometric topology optimization (HITO), including three part:
multilevel mesh, multigrid conjugate gradient method (MGCG) and local-update strategy, which improves the
efficiency in three aspects: mesh scale reduction, solving acceleration and design variables reduction. Four
benchmark examples are used to evaluate proposed method, and the results show that the proposed HITO
successfully reduces 37%–93% computational time compared to the conventional isogeometric topology optimization (CITO) and obtains consistent optimization results, which demonstrates the high-efficiency of
the HITO. Furthermore, the efficiency improvement of the HITO will be more significant for the large-scale
problems.